КИБЕРНЕТИЧЕСКИЙ ПОДХОД К ПРОБЛЕМЕ СУБЪЕКТИВНОГО

На следующее утро я пригласила Кибернетика к себе в съёмную квартиру.

Я наварила ему чая и рассказала ему про своё лечение, и поэтому я спокойно ему поставила вопрос

• Почему люди имеют совершенно иные мнения на тот или иной вопрос. Если они имеют то или иное мнение, то почему они не могут договариваться по тому или иному вопросу. В математике мы разве спорим о том что 2+2=4..

• А почему это так важно..

• Дело в том что, наука я имею в виду точные науки это единственный способ при котором мы сможем договариваться каких-то вещах. В других областях человеческого познания господствует субъективность. А если невозможно договариваться то можно только верить, а любая вера приносится на на кончике меча.

  Кибернетик почесал голову, а потом сказал

• Кибернетический подход к эволюции читали.

  И Кибернетик набрал на своём смартфоне Феномен науки: Кибернетический подход к эволюции

  • 1.8. Нервная сеть

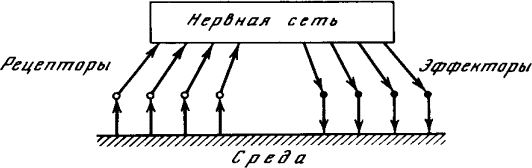
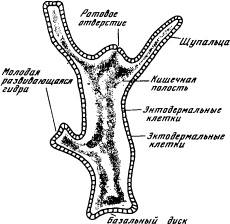
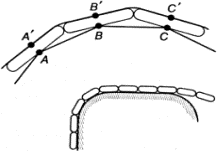
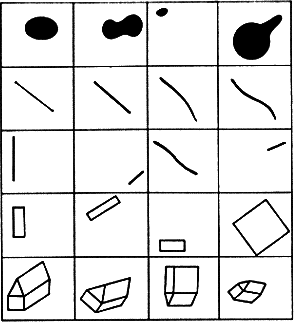
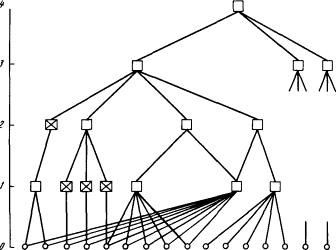
Общая схема нервной системы «кибернетического животного» в его взаимодействии с внешней средой представлена на рис. 1.7. Чувствительные нервные клетки, возбуждающиеся под действием внешних факторов, носят название рецепторов (т. е. получателей), ибо они служат первичным приемником информации о состоянии внешней среды. Эта информация поступает в нервную сеть и перерабатывается ею. В результате возбуждаются некоторые из нервных клеток, называемых эффекторами. Разветвления эффекторных клеток пронизывают те ткани организма, на которые нервная система оказывает непосредственное влияние. Возбуждение эффектора вызывает сокращение соответствующей мышцы или стимулирует деятельность соответствующей железы. Состояние всех рецепторов в некоторый момент времени назовем ситуацией в этот момент. (Точнее было бы говорить «результат воздействия ситуации на органы чувств», но это слишком длинно.) Состояние всех эффекторов назовем действием. Следовательно, роль нервной сети сводится к преобразованию ситуации в действие.

Рис. 1.7. Нервная система «кибернетического животного»

Под «средой» на рис. 1.7 удобно понимать не только предметы, окружающие животное, но также и его костно-мышечную систему и вообще все то, что не входит в состав нервной системы. Это снимает необходимость изображать на схеме отдельно тело животного и «не тело», тем более что никакого принципиального значения для деятельности нервной системы это разграничение не имеет. Важно лишь то, что возбуждение эффекторов приводит к определенным переменам в «среде». При том общем подходе к проблеме, который лежит в основе нашего рассмотрения, нам достаточно квалифицировать эти изменения как «полезные» или «вредные» для животного, не вдаваясь в дальнейшие подробности.

Какова задача нервной системы? Способствовать выживанию и размножению животного. Нервная система работает хорошо, когда возбуждение эффекторов приводит к полезным с этой точки зрения изменениям состояния среды, и плохо — в противном случае. Совершенствуясь в процессе эволюции, нервная система выполняет эту задачу все лучше и лучше. Каким образом это удается? Каким законам подчиняется процесс ее совершенствования?

Мы попытаемся ответить на эти вопросы, выделив в эволюции нервной системы животных несколько этапов, четко отличающихся между собой с кибернетической точки зрения, и показав, что из основного закона эволюции следует неизбежность перехода от каждого предыдущего этапа к каждому последующему. Так как в кибернетическую эру эволюция живых существ — это прежде всего эволюция их нервной системы, периодизация развития нервной системы дает периодизацию развития жизни в целом.

1.9. Простой рефлекс (раздражимость)

Простейший вариант нервной сети — это вообще ее отсутствие. В этом случае рецепторы непосредственно связаны с эффекторами и возбуждение с одного или нескольких рецепторов передается на один или несколько эффекторов. Такую прямую связь между возбуждением рецептора и эффектора мы назовем простым рефлексом.

Этот этап — третий по нашей сквозной нумерации этапов эволюции — является пограничным между химической и кибернетической эрами. Тип кишечнополостных представляет животных, застывших на уровне простого рефлекса. Возьмем, например, гидру, которую изучают в школе как типичного представителя кишечнополостных. Тело гидры (рис. 1.8) имеет вид удлиненного мешочка. Его внутренность — кишечная полость — сообщается с внешней средой через ротовое отверстие, окруженное несколькими щупальцами. Стенки мешочка состоят из двух слоев клеток: внутреннего (энтодерма) и внешнего (эктодерма). И в эктодерме, и в энтодерме много мышечных клеток, содержащих волоконца, которые могут сокращаться, приводя тело гидры в движение. Кроме того, в эктодерме есть и нервные клетки, причем клетки, расположенные ближе всего к поверхности, — это рецепторы, а клетки, заложенные глубже, среди мышц, — эффекторы. Если к гидре прикоснуться иглой, она сжимается в комочек. Это простой рефлекс, вызванный передачей возбуждения от рецепторов к эффекторам.

Рис. 1.8. Строение гидры

Но гидра способна и к гораздо более сложному поведению. Захватив добычу, она подтягивает ее щупальцами к ротовому отверстию и заглатывает. Такое поведение тоже можно объяснить совокупным действием простых рефлексов, связывающих эффекторы и рецепторы локально — в пределах большого участка тела. Например, следующая модель щупальца объясняет его способность обвиваться вокруг падающих предметов (рис. 1.9). Представим себе некоторое количество звеньев, соединенных между собой шарнирами (для простоты рассматриваем плоскую картину). Точки A и B, A' и B', B и C, В' и C' и т. д. соединены между собой тяжами, которые могут сокращаться (мышцы). Все эти точки являются чувствительными, возбуждаясь от прикосновения к предмету (рецепторы). Возбуждение каждой точки приводит к сокращению двух соседних с нею тяжей (рефлекс).

Рис. 1.9. Модель щупальца

1.10. Сложный рефлекс

Простая рефлекторная связь между возбудимой и мышечной клетками естественно возникает в процессе эволюции по методу проб и ошибок: если оказывается, что корреляция между возбуждением одной клетки и сокращением другой полезна для животного, то эта корреляция устанавливается и закрепляется. При механическом копировании связанных клеток в процессе роста и размножения природа получает систему параллельно действующих простых рефлексов, подобную щупальцу гидры. Но когда в ее (природы) распоряжении оказывается множество рецепторов и эффекторов, связанных попарно или локально, у нее «возникает искушение» усложнить систему связей путем введения промежуточных нейронов. Выгодность этого следует из того, что при наличии системы связей между всеми нейронами становятся возможными такие формы поведения, которые невозможны при ограничении парными или локальными связями. Последнее утверждение можно доказать простым подсчетом всевозможных способов преобразования ситуации в действие при том и другом способах связи. Пусть, например, у нас есть n попарно связанных рецепторов и эффекторов. Связь в каждой паре может быть либо положительная (возбуждение вызывает возбуждение, покой — покой), либо отрицательная (возбуждение вызывает покой, покой — возбуждение). Следовательно, всего возможно 2ⁿ вариантов связи, т. е. 2ⁿ вариантов поведения. Если же предположить, что система связей может быть произвольная, т. е. состояние возбуждения или покоя каждого эффектора может произвольным образом зависеть от состояния всех рецепторов, то подсчет всевозможных вариантов поведения приводит к числу 2⁽²ⁿ⁾ⁿ, неизмеримо большему, чем 2ⁿ. Совершенно такой же расчет приводит к заключению, что объединение любых подсистем, связывающих независимо друг от друга группы рецепторов и эффекторов в единую систему, всегда приводит к огромному возрастанию числа возможных вариантов поведения. Поэтому на протяжении всей истории жизни эволюция нервной системы проходит под знаком увеличения централизации.

Однако централизация централизации рознь. Если связать все нейроны в один бессмысленно запутанный клубок, то, несмотря на крайнюю «централизованность» такой системы, она вряд ли будет иметь шансы выжить в борьбе за существование. Централизация ставит следующую проблему: как из всех мыслимых способов соединения многих рецепторов с многими эффекторами (с помощью промежуточных нейронов, если потребуется) выбрать такой способ, который будет каждой ситуации сопоставлять правильное, т. е. полезное для выживания и размножения, действие? Ведь подавляющее большинство способов соединения не обладает этим свойством.

Мы знаем, что каждый новый шаг на пути усложнения живых структур природа делает по методу проб и ошибок. Посмотрим, что дает непосредственное применение метода проб и ошибок к нашей проблеме. Рассмотрим для примера небольшую систему из ста рецепторов и ста эффекторов. Допустим, что в нашем распоряжении сколько угодно нейронов для создания промежуточной нервной сети и что мы умеем легко определять, дает ли данный способ соединения нейронов правильную реакцию на каждую ситуацию. Будем перебирать все мыслимые способы, пока не натолкнемся на нужный. При n = 100 число функционально различных нервных сетей между n рецепторами и n эффекторами есть

2⁽²ⁿ⁾ⁿ ≈ 10⁽¹⁰³²⁾.

Число это невообразимо велико. Перебор такого числа вариантов недоступен не только нам, но и нашей матушке-природе. Если бы каждый атом во всей видимой нами части Вселенной занимался просмотром вариантов и перебирал бы их со скоростью миллиард штук в секунду, то и за миллиард миллиардов лет (а наша Земля существует не более десяти миллиардов лет) не была бы просмотрена и миллиардная доля общего числа вариантов.

Между тем как-то ведь происходит формирование эффективно работающей нервной сети! Причем число рецепторов и эффекторов у высших животных исчисляется не сотнями и не тысячами, а миллионами.

Разгадка кроется в иерархическом строении нервной системы.

Здесь нам снова необходим экскурс в область общекибернетических понятий. Четвертый этап эволюции мы назовем этапом сложного рефлекса, но дать определение этому понятию сможем лишь после того, как познакомимся с некоторыми фактами об иерархически устроенных нервных сетях.

2.1. Понятие понятия

Рассмотрим такую нервную сеть, которая на входе имеет много рецепторов, а на выходе — всего один эффектор, так что нервная сеть делит множество всех ситуаций на два подмножества: ситуации, вызывающие возбуждение эффектора, и ситуации, оставляющие его в покое. Задачу, решаемую в этом случае нервной сетью, называют задачей распознавания (имеется в виду распознавание принадлежности ситуации к тому или иному множеству). Животному в борьбе за существование приходится сплошь и рядом решать задачу распознавания, например: отличить ситуацию, опасную для жизни, от неопасной, отличить съедобные предметы от несъедобных и т. п. Это только наиболее яркие примеры, детальный анализ поведения животного приводит к выводу, что для выполнения сколь-нибудь сложного действия оно должно непрерывно решать множество «мелких» задач распознавания.

Множество ситуаций в кибернетике называют понятием¹. Чтобы лучше уяснить, как кибернетическое понимание слова «понятие» связано с его обычным пониманием, допустим, что рецепторы рассматриваемой нами нервной сети — это светочувствительные нервные окончания сетчатки глаза или же вообще какие-то светочувствительные точки на экране, подающем информацию в нервную сеть. Рецепторы возбуждаются тогда, когда соответствующий участок экрана освещен (точнее, когда его освещенность больше некоторой пороговой величины), и остаются в состоянии покоя — в противном случае. Если на месте каждого возбужденного рецептора представить себе светлую точку, а на месте каждого невозбужденного — темную, то получится картина, которая отличается от изображения, падающего на экран, лишь своей дискретностью (т. е. тем, что она распадается на отдельные точки) и отсутствием полутонов. Будем считать, что точек (рецепторов) на экране достаточно много, а изображения, которые могут оказаться на экране, — их мы будем называть «картинками» — предельно контрастны, т. е. состоят лишь из белого и черного цвета. Тогда каждая ситуация соответствует определенной картинке.

Рис 2.1. Картинки, представляющие различные понятия

Согласно традиционной (аристотелевской) логике, когда мы думаем или говорим о какой-то определенной картинке (например, о той, которая находится в левом верхнем углу на рис. 2.1), то мы имеем дело с единичным понятием. Кроме единичных понятий, есть еще общие, или абстрактные, понятия. Например, мы можем думать о пятне вообще — не о каком-либо конкретном пятне (допустим, из числа изображенных в верхнем ряду на рис. 2.1), а о пятне как таковом. Точно так же мы можем обладать абстрактным понятием прямой линии, контура, четырехугольника, квадрата и т. д.²

Однако что значит «обладать абстрактным понятием»? Как можно проверить, обладает ли кто-то данным абстрактным понятием, например понятием «пятно»? Очевидно, только одним способом: предложить испытуемому серию картинок и попросить, чтобы он о каждой из них сказал, пятно это или нет. Если окажется, что он называет пятном только те и все те картинки, на которых «изображено пятно» (это уже с точки зрения испытующего), то, значит, понятием пятна он обладает. Иначе говоря, мы должны проверить его способность распознавать принадлежность любой предъявленной картинки к множеству картинок, которые мы описываем словом «пятно». Итак, абстрактное понятие в обычном смысле слова — во всяком случае когда речь идет о чувственно воспринимаемых образах — совпадает с введенным нами кибернетическим понятием понятия как множества ситуаций. Поэтому задачу распознавания называют также, желая сделать термин более конкретным, задачей распознавания образов (имеется в виду «обобщенных» образов) или задачей распознавания понятий (имеется в виду распознавание частных случаев понятий).

Множеству, состоящему из одной ситуации (картинки), соответствует в традиционной логике конкретное понятие «данная картинка». Отношения между множествами имеют свои непосредственные аналоги в отношениях между понятиями. Если большими буквами обозначить понятия, а маленькими — соответствующие множества, то дополнение множества a, т. е. множество всех мыслимых ситуаций, не входящих в a, соответствует понятию «не A». Пересечение множеств a и b, т. е. множество ситуаций, которые входят и в a, и в b, соответствует понятию «A и B одновременно». Например, если A — понятие «прямоугольник», а B — понятие «ромб», то «A и B одновременно» — понятие «квадрат». Объединение множеств a и b, т. е. множество ситуаций, которые входят хотя бы в одно из множеств a и b, соответствует понятию «либо A, либо B, либо A и B». Если множество a включает в себя множество b, т. е. каждый элемент множества b входит в множество a, но не наоборот, то понятие B есть частный случай понятия A. При этом говорят, что понятие A более общее (абстрактное), чем понятие B, а понятие B более конкретное, чем A. Например, квадрат есть частный случай прямоугольника. Наконец, если множества a и b совпадают, то понятия A и B по существу тождественны и отличаются, быть может, лишь внешней формой их описания — способом распознавания. Встав на точку зрения кибернетики, т. е. отождествив понятие с множеством ситуаций, мы должны рассматривать перечисленные соответствия не как определение новых терминов, а просто как указание на наличие в нашем языке нескольких пар синонимов.

2.2. Распознаватели и классификаторы

Нервную сеть, решающую задачу распознавания, мы назовем распознавателем, а состояние эффектора на его выходе будем называть просто состоянием распознавателя. Отправляясь от понятия распознавателя, мы введем несколько более общее понятие классификатора. Распознаватель делит множество всех мыслимых ситуаций на два непересекающихся подмножества: A и не A. Можно представить себе деление полного множества ситуаций на произвольное число n пересекающихся подмножеств. Такие подмножества называют обычно классами. Теперь вообразим некую подсистему C, имеющую nвозможных состояний и связанную нервной сетью с рецепторами таким образом, что, когда ситуация принадлежит к i-му классу (i-му понятию), подсистема C приходит в i-е состояние. Такую подсистему вместе с нервной сетью мы будем называть классификатором по множеству n понятий(классов), а, говоря о состоянии классификатора, подразумевать состояние подсистемы C (выходной подсистемы). Распознаватель — это, очевидно, классификатор с числом состояний n = 2.

В системе, организованной по двоичному принципу подобно нервной системе, подсистема C с n состояниями будет, конечно, состоять из какого-то числа элементарных подсистем с двумя состояниями, которые можно рассматривать как выходные подсистемы (эффекторы) распознавателей. Состояние классификатора, следовательно, будет описываться указанием состояний ряда распознавателей. Однако эти распознаватели могут быть тесно связаны между собой как по структуре сети, так и по выполняемой функции в нервной системе, и в этом случае их следует рассматривать в совокупности как один классификатор.

Если не накладывать никаких ограничений на число состояний, то понятие «классификатор» фактически теряет смысл. Действительно, всякая нервная сеть сопоставляет каждому входному состоянию одно определенное выходное состояние; следовательно, каждому выходному состоянию соответствует множество входных состояний, и эти множества не пересекаются. Таким образом, всякое кибернетическое устройство с входом и выходом можно формально рассматривать как классификатор. Придавая этому понятию более узкий смысл, мы будем считать, что число выходных состояний классификатора гораздо меньше, чем число входных состояний, так что классификатор действительно «классифицирует» входные состояния (ситуации) по относительно небольшому числу больших классов.

2.3. Иерархия понятий

На рис. 2.2 приведена схема классификатора, организованного по иерархическому принципу. Иерархия вообще — это такое построение системы из подсистем, когда каждой подсистеме приписывается определенное целое число, называемое ее уровнем, причем взаимодействие подсистем существенно зависит от разности их уровней, подчиняясь некоторому общему принципу. Обычно этот принцип — передача информации в определенном направлении (сверху вниз или снизу вверх) от данного уровня к следующему. В нашем случае рецепторам приписывается нулевой уровень, и информация распространяется снизу вверх. Каждая подсистема первого уровня связана с некоторым числом рецепторов, и ее состояние определяется состояниями соответствующих рецепторов. Точно так же каждая подсистема второго уровня связана с рядом подсистем первого уровня и т. д. На высшем (на схеме — четвертом) уровне находится одна выходная подсистема, которая и выносит окончательный приговор о принадлежности ситуации к тому или иному классу.

Рис. 2.2. Иерархия классификаторов

Из этого определения, которое трудно назвать шедевром ясности мысли, можно все-таки заключить, что общие понятия, которые образуются не путем перечисления единичных объектов, входящих в него, а путем указания ряда признаков, объявляемых существенными, и отвлечения от остальных (несущественных) признаков, можно также считать абстрактными. Мы будем рассматривать только такие общие понятия и будем называть их также абстрактными. Например, абстрактный треугольник — это любой треугольник, независимо от величины его сторон и углов и его положения на экране, следовательно, это абстрактное понятие. Такое употребление термина «абстрактный» имеет место в обиходе, а также в математике. В то же время, согласно учебнику логики, «треугольник», «квадрат» и т. п. суть конкретные общие понятия, а вот «треугольность» и «квадратность», которые им свойственны, это понятия абстрактные. По существу, здесь в ранг логического возводится чисто грамматическое различие, ибо даже с точки зрения сторонника последнего варианта терминологии обладание абстрактным понятием равнозначно обладанию соответствующим общим понятием.

Все подсистемы промежуточных уровней также являются классификаторами. Непосредственным входом k-го уровня служат состояния классификаторов k-1-го уровня, совокупность которых является для него ситуацией, подлежащей классификации. В иерархической системе, содержащей более одного промежуточного уровня, можно выделить иерархические подсистемы, охватывающие несколько уровней. Например, в качестве входных ситуаций для классификатора третьего уровня можно рассматривать состояния всех связанных с ним классификаторов первого уровня. Иерархические системы можно достраивать «вширь» и «ввысь» подобно тому, как из восьми кубиков можно сложить кубик с вдвое большим ребром, а из этих кубиков — еще больший кубик и т. д.

Так как с каждым классификатором связана система понятий, иерархия классификаторов порождает иерархию понятий. Передаваясь от уровня к уровню, информация преобразуется, выражаясь в терминах все более «высокопоставленных» понятий. При этом количество передаваемой информации постепенно уменьшается за счет отбрасывания информации, несущественной с точки зрения задачи, поставленной перед «верховным» (выходным) классификатором.

Поясним этот процесс на примере картинок, изображенных на рис. 2.1. Пусть поставлена задача распознавания «домиков». Введем два промежуточных понятийных уровня. На первом разместим совокупность понятий «отрезки», на втором — понятия «многоугольники». Понятие «домик» окажется на третьем уровне.

Под понятием «отрезки» мы понимаем совокупность понятий «отрезок с координатами концов x₁, y₁ и x₂, y₂», где числа x₁, y₁, x₂, y₂ могут принимать любые совместимые с устройством экрана и системой координат значения. Чтобы быть конкретнее, допустим, что экран содержит 1000 × 1000 светочувствительных точек. Тогда координатами могут служить десятиразрядные двоичные числа (2¹⁰ = 1024 > 1000), а отрезок с заданными концами требует для своей характеристики четыре таких числа, т. е. 40 двоичных разрядов. Всего, следовательно, существует 2⁴⁰ таких понятий. Их-то и должны различать классификаторы первого уровня.

Не надо думать, что отрезок с заданными концами — конкретное понятие, т. е. множество, состоящее из одной картинки. Классифицируя предъявленную картинку как отрезок с заданными концами, мы отвлекаемся от незначительных искривлений линии, вариаций ее толщины и т. п. (см. рис. 2.1). Критерий того, какие отклонения от нормы нам следует считать незначительными, может устанавливаться по-разному. Сейчас это нас не интересует.

Каждый классификатор первого уровня должен иметь на выходе подсистему из 40 двоичных разрядов, на которых «записаны» координаты концов отрезка. Сколько нужно классификаторов? Это зависит от того, какие картинки ожидаются на входе системы. Допустим, что для описания любой картинки достаточно 400 отрезков. Значит, достаточно 400 классификаторов. Разделим этот экран на 400 квадратов (50 × 50 точек) и свяжем с каждым квадратом классификатор, который будет фиксировать ближайший к нему, в каком-то смысле (детали разделения труда между классификаторами несущественны), отрезок. Если отрезка нет, пусть классификатор принимает какое-то стандартное «бессмысленное» состояние, например: все четыре координаты равны 1023.

Если предъявить нашей системе картинку, на которой изображено сколько-то отрезков, то соответствующее число классификаторов первого уровня укажет координаты концов отрезков, а остальные примут состояние «нет отрезка». Это и есть описание ситуации в терминах понятий «отрезки». Сравним количество информации на нулевом и на первом уровнях. На нулевом уровне нашей системы 1000 × 1000 = 10⁶ рецепторов получают информацию в миллион бит. На первом уровне 400 классификаторов, каждый из которых содержит 40 двоичных разрядов, т. е. 40 бит информации, всего 16 000 бит. При переходе на первый уровень количество информации уменьшилось в 62,5 раза. Система сохранила ту информацию, которую она сочла «полезной» и отбросила информацию «бесполезную» с ее точки зрения. Относительность этих понятий видна из того, что если предъявленная картинка не соответствует иерархии понятий системы распознавания, то реакция системы будет неправильной или просто бессмысленной. Если, например, на картинке более 400 отрезков, то не все отрезки будут зафиксированы, а если предъявить картинку с пятном, то реакция на нее будет такая же, как на пустую картинку.

Совокупность понятий «многоугольники», занимающую второй уровень иерархии, мы делим на две меньших совокупности: равнобедренные треугольники и параллелограммы. Из числа параллелограммов мы выделяем в особую совокупность прямоугольники. Считая, что для задания угла и длины надо столько же бит (10), как и для координаты, находим, что для задания определенного равнобедренного треугольника надо 50 бит информации, параллелограмма — 60 бит, прямоугольника — 50 бит. Соответственно этому должны быть сконструированы классификаторы второго уровня. Легко видеть, что вся нужная им информация имеется в наличии на первом уровне. Наличие многоугольника констатируется при наличии нескольких отрезков, находящихся между собой в определенных отношениях. При переходе на второй уровень происходит дальнейшее сжатие информации. Отводя из полного числа 400 отрезков по одной трети на каждый вид многоугольников, получаем систему, способную зафиксировать 44 треугольника, 33 прямоугольника и 33 параллелограмма (одновременно). Ее информационная емкость 5830 бит, т. е. почти втрое меньше, чем емкость первого уровня. Зато перед неправильным треугольником или четырехугольником система встанет в тупик!

Понятие «домик» легко описать на языке понятий второго уровня. Домик состоит из четырех многоугольников: одного прямоугольника, одного равнобедренного треугольника и двух параллелограммов, находящихся в определенных отношениях друг к другу (основание равнобедренного треугольника совпадает с одной стороной прямоугольника и т. д.).

Во избежание недоразумений следует указать, что иерархия понятий, о которой мы говорим, имеет гораздо более общий смысл, чем иерархия понятий по абстрактности (общности), которую часто называют просто «иерархия понятий». Примером иерархии по общности может служить пирамида понятий, относящихся к систематике животных. На нулевом уровне располагаются отдельные особи животных («конкретные» понятия), на первом — виды, на втором — роды, затем — семейства, отряды, классы, типы. На вершине пирамиды находится понятие «животное». Такая пирамида является частным случаем иерархии понятий в общем смысле, отличающимся тем, что каждое понятие k-го уровня образуется из некоторого числа понятий k-1-го уровня путем их объединения. Это соответствует очень просто устроенным классификаторам. В общем случае классификаторы могут быть устроены как угодно. Распознаватели, нужные животному, — это скорее иерархии по сложности и тонкости понятий, а не по общности.

2.4. Как возникает иерархия

Вернемся снова к эволюции нервной системы. Может ли иерархия классификаторов возникнуть эволюционным путем? Очевидно, может, но при одном условии: если создание каждого нового уровня иерархии и его последующего расширения полезны животному в борьбе за жизнь. Из факта существования животных с высокоорганизованной нервной системой мы делаем вывод, что так оно и есть в действительности. Кроме того, изучая примитивных животных, мы видим, что система понятий, которые способна распознавать их нервная система, также весьма примитивна. Следовательно, в пользе нижайшего уровня иерархии классификаторов мы убеждаемся воочию.

Набросаем в общих чертах путь развития нервной системы. На начальных стадиях мы находим у животного всего несколько рецепторов. Число возможных способов связи между ними (соединений) относительно невелико и допускает прямой перебор. По методу проб и ошибок находится выгодное соединение. То, что выгодное соединение может существовать даже при очень малом числе нейронов, легко видеть на таком примере. Пусть есть всего два светочувствительных рецептора. Если они расположены на разных сторонах тела, то информация, которую они дают (разность освещенностей), достаточна, чтобы животное могло двигаться на свет или против света. Когда выгодное соединение найдено и осуществлено, допустим, с помощью одного промежуточного нейрона (такие нейроны называются ассоциативными), вся группа в целом может быть размножена. Так возникает система ассоциативных нейронов, регистрирующих, например, разности между освещенностями рецепторов и суммирующих эти разности (рис. 2.3).

Рис. 2.3. Простейшие типы связей между рецепторами

Может быть размножена также любая часть системы связанных нейронов, например, один или несколько рецепторов. Тогда возникает система связей типа изображенной на рис. 2.3,б. Схемы обоих типов образуют в совокупности первый уровень иерархии, основанный на понятиях суммы и разности освещенностей. Поскольку для корректировки движения животного очень важно регистрировать изменение освещенности в данной точке со временем, можно предположить, что на самых ранних стадиях должны появиться нейроны, срабатывающие при изменении освещенности в точке. Это может быть как рецептор, так и ассоциативный нейрон, связанный с одним или несколькими рецепторами. В общем виде можно охарактеризовать классификаторы первого уровня как регистрирующие суммы и разности возбуждений рецепторов в пространстве и времени.

Доказав свою полезность для животного, классификаторы первого уровня прочно входят в число его средств борьбы за существование. Тогда начинается следующая серия проб и ошибок: небольшое число классификаторов первого уровня (точнее, их выходных подсистем) связывается между собой в один пробный классификатор второго уровня, пока не получится полезное соединение. Затем оказывается полезным размножение этого соединения. Можно предположить, что на втором уровне иерархии — поскольку это касается органов зрения — появляются такие понятия, как граница между светом и тенью, средняя освещенность пятна, движение границы между светом и тенью и т. п. Таким же путем возникают и следующие уровни иерархии.

Набросанная нами схема наводит на мысль, что любая сложная система, возникшая в процессе эволюции по методу проб и ошибок, должна иметь иерархическую организацию. Действительно, не имея возможности перебрать все мыслимые соединения большого числа элементов, природа перебирает соединения из нескольких элементов, а найдя полезную комбинацию, размножает ее и использует как целое в качестве элемента, который может быть связан с небольшим числом других таких же элементов. Так и возникает иерархия. Это понятие играет огромную роль в кибернетике. Фактически всякая сложная система, как возникшая естественно, так и созданная человеком, может считаться организованной, только если она основана на некой иерархии или переплетении нескольких иерархий. Во всяком случае, до сих пор мы не знаем организованных систем, устроенных иначе.

Кибернетик взял паузу.

​